In set theory and other branches of mathematics, the union of a collection of sets is the set that contains everything that belongs to any of the sets, but nothing else. If A and B are sets, then the union of A and B is the set that contains all elements of A and all elements of B, but no other elements. The union of A and B is usually written "A ∪ B".
That's not what I though union would be, intuitively. What I thought would be the union, is the intersection:
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements. The intersection of A and B is written "A ∩ B".
Also interesting is symmetric difference:
symmetric difference of two sets is the set of elements which are in one of the sets, but not in both. This operation is the set-theoretic equivalent of the exclusive disjunction (XOR operation) in Boolean logic. The symmetric difference of the sets A and B is commonly denoted by
The symmetric difference is equivalent to the union of both relative complements, that is:
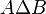



4 comments:
I love set theory.
ndjke
I was seriously just about to post, "I love this shit."
How weird is that?
I've only dabbled my toes in the set theory waters, but I think I like.
Something our Algebra teacher said was interesting. He mentioned that when he went to K-12, they didn't talk about sets. He's probably in his 50's. I wonder if that was a general curriculum thing?
I'm not 100% sure we did sets in high school, it might have been college. I have a hard time now figuring out what went where in my education from 2nd grade to now. I only have K-2nd figured out because Margot's in 2nd grade now.
kfqyoi
Post a Comment