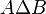Mechanizing inference

A couple years ago I sat down, with great expectation, to read David Berlinski's _The Advent of the Algorithm_. Long story short, it was a frustrating and disappointing experience. I couldn't decide if the book was just bad, or if I just didn't get it.

Recently I picked it back up. I pinpointed where my frustration started, page 10. I didn't get it, and was lost from there on. Berlinski starts his story about the origins of the idea of the algorithm, with Leibniz and his work in logic. According to Berlinski, very little had happened in formal logic since Aristotle and his syllogisms. With the syllogism, Aristotle codified inference.

• All men are mortal
• Socrates is a man
• Therefore, (I can infer that) Socrates is mortal

The nagging question is, what really happens in my mind when I infer. How do you describe that procedure in a way that doesn't rely on an intuitive human understanding? I gather from the book that Leibniz pondered this and ended up describing it with algebraic logic. Berlinski then gives an example. The example never made sense to me. I won't incude it here. I'm sure its correct, it just never clicked for me, no matter how much I looked at it. This was driving me nuts, until I went looking for an alternative that I could grok. I found one which I will steal from the wikipedia article, First-order logic. ∀x φ(x) means that φ(a) is true for any value of a.

• ∀ x (Man(x) → Mortal(x))
• Man(Socrates)
• ∴ Mortal(Socrates)

This makes it clear to me that the inferential step is substitution.

That, of course, is what Berlinski's example in the book shows, only I couldn' t follow it. The reason it is important is that it means inference can be achieved with a mechanical procedure of substitution.

Lucid geometry

Lucid dreaming
Euclid geometry

---------------symmetry +++++++ order

Guide your fantasy

My new self-help program, "Lucid Purposing"

oneironauts (literally from the Greek ονειροναύτες, meaning "dream sailors")

suffused with light

fearlessflyer

My nom de plume over at ficlets.com is fearlessflyer. See all my ficlets at http://ficlets.com/authors/fearlessflyer

snap snap clappiness

Happiness snap snap clappiness silly putty

greatest happiness principle as a guide for ethical behavior

~~~~~~~~~~~~~~~~~~purpose?

Bluebird ++++++++ birds of a feather

mudluscious

Happiness is a warm gun.

Difficulties in defining internal experiences.


Money is the root of all ????

Albert Schweitzer:

Happiness is nothing more than good health and a bad memory.

prose rose

purpose repurpose propose prose rose

According to some philosophies, purpose is central to a good human life.
.
.
.
Purpose is similar to teleology, the idea that a final goal is implicit in all living organisms
http://en.wikipedia.org/wiki/Purpose

-----------------------------------------_The Purpose Driven Life_

Dictionairy of the History of Ideas

Eat, sleep, reproduce, eat, sleep, reproduce, eat, sleep, reproduce, eat, sleep

Don't worry,
&&&&&&&&be happy

Ecclesiastes ~~~~~~~I dream ++++++++++what's the payoff?

Partner

Life is like a roll of toilet paper

Symbol: ∪

From wikipedia:

In set theory and other branches of mathematics, the union of a collection of sets is the set that contains everything that belongs to any of the sets, but nothing else. If A and B are sets, then the union of A and B is the set that contains all elements of A and all elements of B, but no other elements. The union of A and B is usually written "A ∪ B".

That's not what I though union would be, intuitively. What I thought would be the union, is the intersection:

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements. The intersection of A and B is written "A ∩ B".

Also interesting is symmetric difference:

symmetric difference of two sets is the set of elements which are in one of the sets, but not in both. This operation is the set-theoretic equivalent of the exclusive disjunction (XOR operation) in Boolean logic. The symmetric difference of the sets A and B is commonly denoted by

The symmetric difference is equivalent to the union of both relative complements, that is:

Union City Man

Union. It pops up again as I'm listening to ... Blondie, of course.

Oh power, passion plays a double hand
Union, Union Union City man

--Blondie, Union City Blue

Ficlets

My brother Luke pointed me to www.ficlets.com. You write something very short, release it into the wild, and see if anyone writes a prequel or sequel. Or you start with something that's already there and write a prequel or sequel. It's bite size, its tasty, its fun. I have contributed my first ficlet, Weed.

Haunted by words

Do you ever become fascinated by a particular word? Entranced? Haunted? Do they take on the power of incantation? Recently the word, "union," is always slipping around in the shadows of my mind, darting in and out of my peripheral vision.

Mantra

Stand up straight, don' t be afraid.

Borrowed Words (from a Has Been)

I know exactly what she's going to do,
And I can't wait for her to do it.
--William Shatner, "Familiar Love"

My footsteps here don't matter

I could write volumes about the hike I just took in the foothills of the Sandia Mountains, about 30 minutes from my home. These are the kind of stream-of-consciousness notes I jotted down while out there.

Decomposing leaf in stream becoming transparent

Cool breeze off stream
Granite is slippery when wet
Red willow branches

Water in many forms, snow, ice, running water

Many little channels in one stream

Stream disappears

The heat of my body, the chill of the air, the stream, the ice

True shapes

Snow that hasn't forgotten itself

My footsteps here don' t matter

Thick as a Brick

One of the best movies I almost never saw. I've never seen any promotion for it or read any reviews. Pure word of mouth. Amusing idea brilliantly executed. See it.
Brick.

Word problems

Jae and I are taking a very basic algebra class at Central New Mexico Community College. Early in the course, we reached the first word problems in the text book. The teacher was going over the first one thoroughly in class. The word problem was about making bicycles, and producing a table that showed how many tires you needed to order if you were making x bicycles.

Jae and I have been enjoying passing notes to each other in class. Makes us feel young, I guess. Jae passed me a note that said:

For each bicycle, how many pairs of tight lycra pants do you need?

I made the problem more complex and passed it back:

If you have 100 bicylces, and 20 of the riders each have a nice ass, how many pairs of baggy shorts do you need?

I can see a whole passtime of writing amusing word problems.